4 Auguest 2024

Using Monte Carlo Tree Search in for AI in Indix Infernalis

In this post i'm going to go over how I used the Monte Carlo Tree Search algorithm in my game "Indix Infernalis" and provide some C++ code examples to supplement the more abstract academic literature out there.

What is Indix Infernalis

Indix Infernalis is the (unofficial & fan-made) videogame version of Magnagothica Maleghast, programmed solely by me. Magnagothica Maleghast is a tabletop skirmish wargame made by Tom Bloom.

What is Monte Carlo Tree Search (MCTS)

Monte Carlo Tree Search is a heuristic tree-search that is often used to power game playing AI. It is a key part of the famous Go playing system AlphaGo. What makes MCTS desirable in my case (and others) is it is able to deal with very high "branching factors" (meaning, how many options does a player have at each given game state) in a game.

The algorithm iteratively builds a tree of possible future states from a given starting or root state using random choice selection, with each edge between nodes being a distinct choice or action. This iterative process can be broken up into four steps: Simulation, Back-Propogation, Selection, & Expansion

Below is a basic node in the tree that we will be iteratively building. This struct definition will be used in future examples

	struct Node {
		Node* parent;
		void* gameState;

		Node* nextSibling;
		Node* firstChild;

		Int wins;
		Int visits;

		float heuristicScore;
		float GetUCBValue();
		bool IsNotEndNode();
	};
	

Simulation

As the name implies, this step plays out a game from a starting state to an end state making random choices during each turn. The sequence of choices is frequently referred to as a "roll-out" or "play-out" in other literature.

Below is a basic simulation loop. "Game::Step()" advances our game state after selecting an input until another input is requested.

	bool* keepBuilding;
	while( *keepBuilding ) {
		TreeNode* current = rootNode;

		// Simulate until end node is reached
		while( current->IsNotEndNode() ) {
			InputOptions options = GetInputOptions();

			int randomSelectionIndex; //...
			InputSelection selection = options.GetSelectionByIndex( randomSelectionIndex );
			
			Game::CompeteInput( selection );
			Game::Step();

			current = CreateNewNodeFromCurrentState();
		}

		Int winnerValue; // calculate winner here
		BackPropogate( current, winnerValue );

		// Select a new node to start from, reset the state
		// and do the whole thing over again
		current = SelectNewNode();
		Game::SetState( current->gameState );
	}
	

Back-Propagation

Once an end-game state has been reached (tie/win/loss), the algorithm travels back up the tree from the leaf node it arrived at all the way back to the root node. It stops at each node along the way a notes that the node was visited (i.e. it was part of a rollout) and accumulates the outcome (incrementing a counter for wins, decrementing for losses). The bulk of the algorithm's computation time is spent in this and the simulation. Across many such runs, MCTS builds up win ratio statistics, which is used in the next step.

	void BackPropogate( TreeNode* node, int winValue ) {
		node->wins += winValue;
		node->visits += 1;

		if( node->parent != NULL ) {
	    	BackPropogate( node->parent, winValue );
		}
	}
	

Selection

This step is where the algorithm gets its "heuristic" attribute. When it comes time to choose another starting node MCTS aims to strike a balance between "exploring" new roll-outs and "exploiting" promising ones. It does this by an upper confidence bound or UCB function performed on each child node. The child node with the highest value is moved to and the search repeats until a node without children is reached. There is a great deal of literature about UCB functions but below is my implementation of it.

	float Node::GetUCBValue() {
		// If possible, empty nodes should be selected
		if( visits == 0 || parent == NULL ) {
	    	return FLT_MAX;
		}

		float nodeVisits = (float)visits;

		float exploitationTerm = (heuristicScore  + wins ) /
	    	nodeVisits;

		float parentVisits = parent->visits;

		float explorationTerm = explorationParam * sqrt(
	    	logf( parentVisits ) / nodeVisits
		);

		float selectionValue = exploitationTerm + explorationTerm;
		 
		return selectionValue;
	}

	TreeNode* SelectNewNode() {
		bool nextExpansionNodeFound = false;
		TreeNode* node = rootNode;
		do {
	    	float highestUCB = -FLT_MAX;
	    	TreeNode* bestChild = node->firstChild;
	    	TreeNode* childNode = node->firstChild;
	    	while( childNode != NULL ) {
	        	float UCB = childNode->GetUCBValue();
	        	if( highestUCB < UCB ) {
	            	bestChild = childNode;
	            	highestUCB = UCB;
	        	}
	        	childNode = childNode->nextSibling;
	    	}

	    	node = bestChild;

	    	// Check if this is an empty node
	    	nextExpansionNodeFound = node->firstChild == NULL;
		} while( !nextExpansionNodeFound );

		return node;
	}
	

Expansion

Once a node is selected, we generate empty child nodes for each possible input. One of these will be our next starting simulation state (selected randomly). It's worth mentioning that we don't store any nodes built during the game simulation step.

	Struct GameState {
		UnitInstance unitStateStorage [ MAX_UNITS ];
		tgObject objectStateStorage[ MAX_OBJECTS ];
		
		Space spaces [ MAX_MAP_SIZE ][ MAX_MAP_SIZE ];

		Int round;
		// Other game state omitted here
		// ...
	};
	

Implementation Hiccups

Of course, no problem ever follows theoretical paths exactly. I ran into a few degenerate cases that had to be worked around in special cases.

Redundant States

Sometimes, actions can fail to execute in Indix Infernalis. This is, unfortunately, a fact of how i've implemented the rules of the game. If I could do it over i'd find a way to avoid this possible error state but it was something I had to live with and handle if I wanted to avoid infinite loops. What I was finding in early development was game simulation getting trapped in a loop it couldn't escape by selecting a particular input that would result in no change of state (and therefore, nothing to prevent the AI from selecting the same input again...and again, etc.). The solution I arrived at was to keep a hash of the gamestate in each node, and as each node is created, its hash is checked against each node in it's chain of parents back to the root. When a redundant state is detected tree building is rewound back to the last node that has unexplored children.

Results

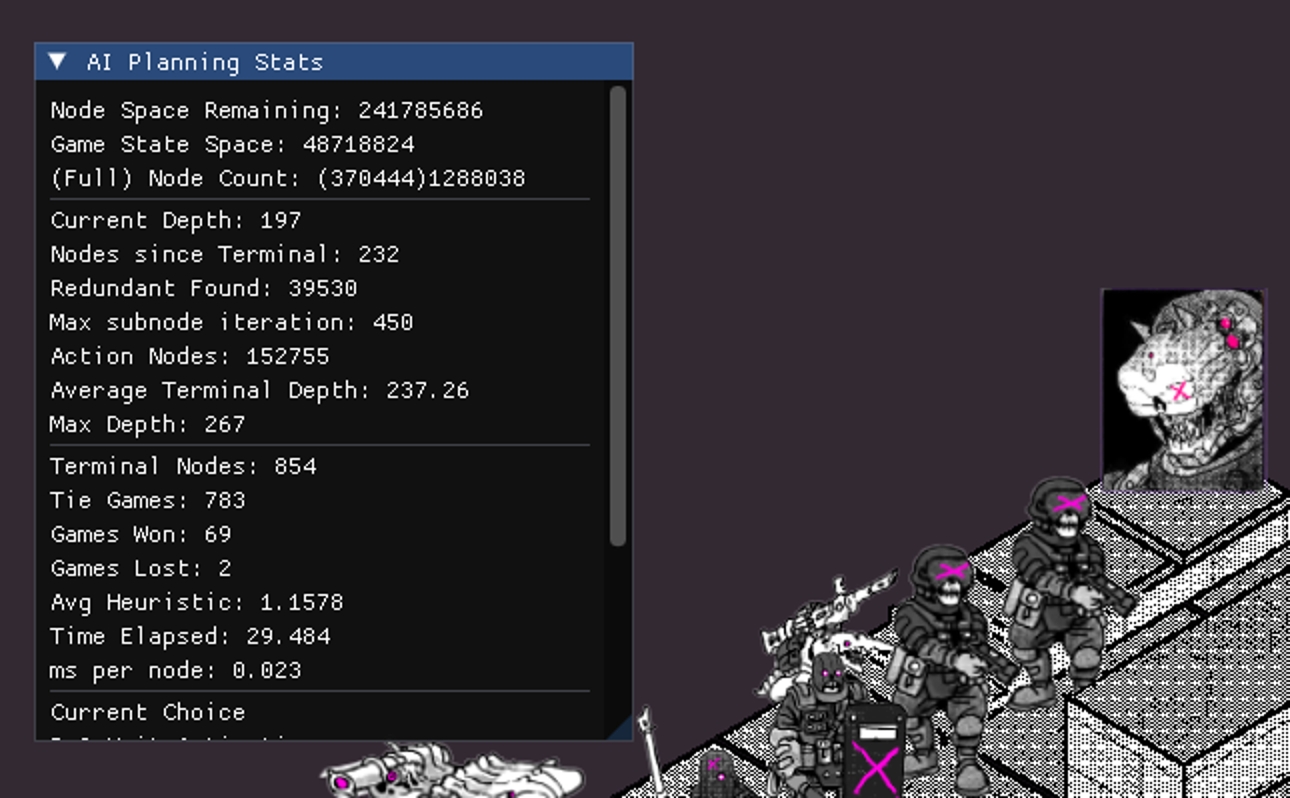
As of this writing, on a 12th Gen Intel i5 this system processes 370k game states in 30 seconds, reaching 854 full playouts. With this computational power, it is able to perform reasonably in favorable conditions. Performance profiling results show that the majority of the remaining computation time is inside the game state "Step" function, which would likely be time consuming to improve.

Plans for further development

Given that most of the computation time is spent in our game's "Step" function, the easiest improvement will be parallelizing the search. MCTS already has some robust academic research around parallelization structures. Additionally, what i've written here does not cover the integration of expert knowledge. Like many games, Magnagothica has situations where there are many possible moves, but only a few reasonably profitable ones. I have plans for further improvements, however, so if you're interested stay tuned.